이숭간 공부기록
[프로그래머스] 파이썬 _ 정수 삼각형 본문
728x90
https://programmers.co.kr/learn/courses/30/lessons/43105
코딩테스트 연습 - 정수 삼각형
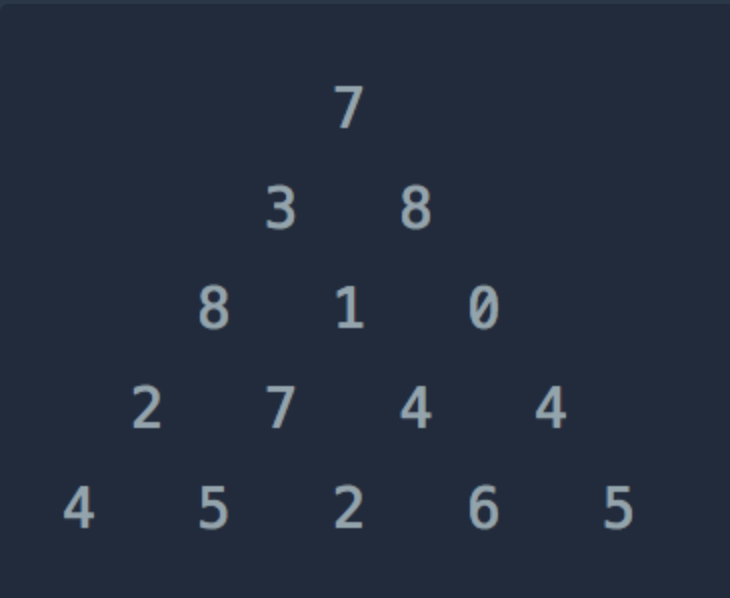
[[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] 30
programmers.co.kr
문제유형 : DP
문제풀이 :
- 이문제가 왜 DP인가? (DP의 조건 : 1. 최적부분구조, 2. 중복되는 부분문제)
- 현재위치의 가장 큰값은 윗 줄의 가장큰값이 필요하다. 즉 특정 번째까지의 최적해는 앞의 최적해를 이용한다. ( 최적부분구조 )
- 특정위치의 값을 구할때 대각선 위 값들을 비교하여 찾아낸다. 이것이 계속 반복된다. ( 중복되는 부분문제 )
- 현재위치에서 가장큰 합을 저장하는 배열을 new_val이라고 했을때
- new_val[i][j] = triangle[i][j] + max(new_val[i-1][j-1], new_val[i-1][j])
- 즉, 현재값 + 위에서 내려올수있는 가장 큰값을 더한값이 현재위치에서 최대합이 된다.
- 이때 인덱스 에러가 나지않게 조건만 잘 검색해주면 된다.
정답코드 :
answer = 0
def solution(triangle):
global end
end = len(triangle)
start_node = triangle[0][0]
new_val = [[] for _ in range(end)]
# 최대합을 저장할 2차원 리스트
new_val[0].append(start_node)
for i in range(end):
for j in range(len(triangle[i])):
curr = triangle[i][j]
# 맨 윗줄이면 그냥 넘어간다.
if i == 0:
continue
# 대각선 위로 2개가 존재하는 경우 둘중에 더 큰값을 더한다.
if j > 0 and j < len(triangle[i])-1:
val = max(new_val[i-1][j-1], new_val[i-1][j])
curr += val
# 오른쪽 위 대각선만 존재하는 경우
elif j == 0:
curr += new_val[i-1][j]
# 왼쪽 위 대각선만 존재하는 경우
elif j == len(triangle[i])-1:
curr += new_val[i-1][j-1]
# 구한 현재까지 최대합을 저장한다.
new_val[i].append(curr)
# 최종적으로 맨 마지막줄에서 최댓값이 구할수있는 최대합이다.
return max(new_val[-1])
번외) 사실 이문제를 처음에 DFS로 그냥 풀었다. ㅋㅅㅋ 풀면 답은 나오는데 시간초과가 났다,,,
DFS를 해가면서 이때 다음라운드로 넘어갈때 두개씩만 주면서 풀었다.
굳이 DFS가 거쳐간 경로를 구해야 하는것이 아니면 이런방법은 지양해야겠다.
result = 0
answer = 0
def solution(triangle):
global end
end = len(triangle)
start_node = triangle[0][0]
dfs(0, 0, start_node, triangle, 0, [])
return result
def dfs(start_depth, index, start_node, graph, depth, curr):
curr.append(start_node)
global answer, end, result
answer += start_node
if depth == end - 1:
result = max(result, answer)
return
start_depth += 1
for idx, i in enumerate(graph[start_depth][index : index+2]): # [3,8]
dfs(start_depth, index+idx, i, graph, depth + 1, curr)
answer -= curr.pop()
solution([[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]])
###############################################
[7, 3, 8, 2, 4]
24
[7, 3, 8, 2, 5]
25
[7, 3, 8, 7, 5]
30
[7, 3, 8, 7, 2]
27
[7, 3, 1, 7, 5]
23
[7, 3, 1, 7, 2]
20
[7, 3, 1, 4, 2]
17
[7, 3, 1, 4, 6]
21
[7, 8, 1, 7, 5]
28
[7, 8, 1, 7, 2]
25
[7, 8, 1, 4, 2]
22
[7, 8, 1, 4, 6]
26
[7, 8, 0, 4, 2]
21
[7, 8, 0, 4, 6]
25
[7, 8, 0, 4, 6]
25
[7, 8, 0, 4, 5]
24
30
Process finished with exit code 0
'알고리즘 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 파이썬 _ 소수찾기 (0) | 2021.07.07 |
|---|---|
| [프로그래머스] 파이썬 _ 수식 최대화 (2020 KAKAO INTERN) (0) | 2021.07.05 |
| [프로그래머스] 파이썬 _ 2 x n 타일링 (0) | 2021.07.04 |
| [프로그래머스] 파이썬 _ 체육복 (0) | 2021.07.03 |
| [프로그래머스] 파이썬 _ 불량 사용자 (2018 KAKAO WINTER INTERN) (0) | 2021.07.03 |

